Vikarpakker i statistik

Få fagligt udbytte af vikartimer - uden forberedelse for vikar eller lærer. Vælg et af 5 temaer (1-2 lektioner) med statistik fra Danmarks Statistik om emner tæt på eleverne og interaktive opgaver med gæt og refleksion.

Kapitler

Kapitel 1

Hvor mange deler jeg navn med? (1 lekt.)

Søg på dit navn og se, hvor mange der hedder det samme som dig
Hvor mange hedder
Søg på dit navn og se, hvor mange der hedder det samme som dig

Opgaver

  1. Hvor mange danskere har det samme navn som dig?
  2. Lav et søjlediagram, der viser antallet af danskere med hver af gruppens navne
  3. Hvor mange danskere deler jeres gruppe i gennemsnit navn med?  Se eksempel på beregning nedenunder.

Beregning af gennemsnit

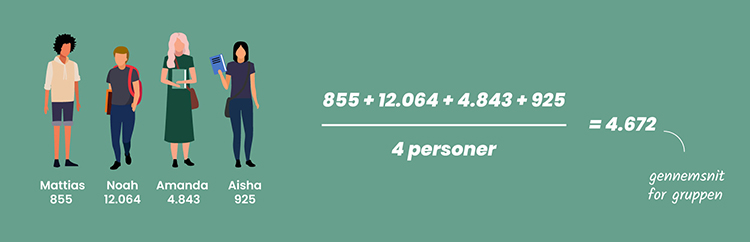
Eks. på beregning af gennemsnit

Ligesom mode skifter for tøj, ændrer navne også popularitet. Se udviklingen i, hvilke navne danskerne har givet deres børn siden 1985.
Navnebarometer
Ligesom mode skifter for tøj, ændrer navne også popularitet. Se udviklingen i, hvilke navne danskerne har givet deres børn siden 1985.

Opgaver

Klik på grafikken ovenover, og gå ind på opgørelsen over babynavne siden 1985. Se om flere eller færre får dit navn nu, end det år, hvor du blev født.

  1. Bliver jeres navne i gruppen mere eller mindre udbredte?
  2. Tjek 3 af jeres læreres navne: Går de frem eller tilbage?
  3. Hvorfor tror I, at navne bliver mere eller mindre populære at give til sine børn over tid? 

Kapitel 2

Familier på tværs (2. lekt.)

 

I dag bor unge i mange forskellige typer familier. Nogle har søskende - og deler begge forældre eller en af dem, nogle bor sammen med deres forældre eller en af dem – måske med en ny kæreste. Grafen herunder viser udviklingen i 0-17-åriges familier siden 2008. I kan vælge at lave søjler eller kurver og se værdierne ved at markere dem.

Opgaver

Klik de forskellige variable fra og til og undersøg:

  1. I grafen finder I seks forskellige familietyper, et barn kan indgå i, og 8 forskellige kombinationer af søskende. Find på skift jer selv i opgørelsen.
  2. Hvem af jer har en kombination af familietype og søskende med den største hyppighed det seneste år?
  3. Hvem af jer har en kombination af familietype og søskende med den laveste hyppighed det seneste år?
  4. Find en kombination af søskende, der er kommet flere af i perioden, og find også en, der er kommet færre af. Har I et bud på hvorfor de er steget/faldet?
  • Helsøskende betyder søskende med samme mor og far
  • Halvsøskende betyder søskende med enten samme mor eller samme far.
  • Papsøskende betyder børn, som ikke er biologisk beslægtede, men som bor i samme familie som den ene af barnets biologiske forældre.

Stor eller lille udvikling?

De valg, man træffer, når man viser sine data i et diagram, er vigtige for, om modtageren får indtryk af en stor eller lille udvikling. I eksemplet nedenfor kan du trække i pilen og sammenligne to forskellige grafer, der viser, hvor mange der bor alene. De to grafer viser de samme tal. 

Opgaver

5. Hvad er forskellen på de to diagrammer?

6. Hvilke fordele kan der være ved at vise data på hver af de to måder? Hvorfor?

7. En graf kan give et misvisende indtryk. Hvilke interesser kunne politikere, sociale medier osv. have i det.

8. Hvorfor tror I, at udviklingen af familier på 1 person er, som den er?

9. I Danmark og store dele af verden får familierne færre børn end tidligere. Det betyder, at det på sigt bliver sværere at opretholde befolkningens størrelse. Kan I tænke på 2 områder, hvor det kan give problemer i fremtiden, at der kommer færre nye borgere til? 

Ændringer i familiemønstrene betyder blandt andet, at der er flere par med to af samme køn. Ægteparrene i grafen nedenunder kan både være par, der har indgået et "registreret partnerskab" og par, der er gift. Men hvordan er udviklingen udvikling er gået siden 1986?

Gæt selv, og tegn en graf med jeres bud på udviklingen. I cirkeldiagrammet kan I se, hvor stor en procentdel af jeres svar der rammer rigtigt.

Klasseopgave genemsnit og median

Hvor mange børn er der i jeres familie, hvis I både tæller hel-, halv- og papsøskende - og både hjemme hos far og mor, hvis de ikke bor sammen?

  1. Beregn gennemsnittet af børn i familien i jeres klasse, se grafikken nedenfor. 
  2. Find også medianen ved at stille alle observationer op på en række efter størrelse og vælge den midterste. Hvis der er et lige antal observationer, tager I gennemsnittet af de to midterste.
  3. Er medianen og gennemsnittet ens? Hvis ikke, hvorfor tror I, der er forskel? I kan støtte jer til tekst og grafik under denne opgave.

Beregning af gennemsnit

Eks. på beregning af gennemsnit

Gennemsnit eller median?

Meget store eller små værdier påvirker gennemsnittet meget. Det er godt til at sammenligne grupper med hinanden, men siger ikke noget om fordelingen i datasættet. Medianen er den midterste observation, når et datasæt er sorteret efter størrelse. Den er god at vise, hvis observationerne er fordelt meget skævt.

Fx kan få personer med en meget høj indkomst trække gennemsnittet op, så man ikke opdager, at de fleste har lav indkomst. Det viser medianen.

Gennemsnit og median kan supplere hinanden til at forstå et datasæt.

Kapitel 3

Unge og ældre i min kommune (1-2 lekt.)

 

Mens mange andre lande bruger folketællinger til at tælle befolkningen, har vi CPR-registret i Danmark. Derfor ved vi præcis, hvor mange mennesker der bor i landet – og i de enkelte kommuner.

Grafen viser, hvor mange der bor i alle de danske kommuner, og hvor mange der er i de enkelte aldersgrupper. I kan vælge at lave søjler eller kurver og se værdierne ved at markere dem.

Opgaver

1. Hvor mange mennesker på jeres aldersgruppe tror I, der bor der i jeres kommune?

2. Undersøg tallet og se, hvor stor en %-del af kommunens befolkning jeres aldersgruppe udgjorde sidste år (se evt. forklaring i grafikken nedenunder)?

3. Sammenlign med andelen (%-del) af ældre på 70+. Er der flere eller færre?

4. Hvordan har kommunens befolkning udviklet sig siden 2008?

5. Vælg en kommune i den anden ende af landet og sammenlign andelen afl 10-19-årige og andelen af ældre på 70+ med jeres kommune. Hvad tror I, det kan skyldes, hvis der er forskel på andelene?

 

 

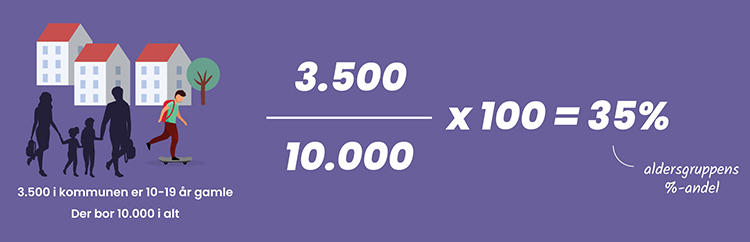
Beregning af procentandel

 

Stor eller lille udvikling?

De valg, man træffer, når man viser sine data i et diagram, er vigtige for, om modtageren får indtryk af en stor eller lille udvikling. I eksemplet nedenfor kan du trække i pilen og sammenligne to forskellige grafer, der viser, hvor mange der er blevet født hvert år. De to grafer viser de samme tal. 

Opgaver

6. Hvad er forskellen på de to diagrammer?

7. Hvilke fordele kan der være ved at vise data på hver af de to måder? Hvorfor?

8. En graf kan give et misvisende indtryk. Hvilke interesser kunne politikere, sociale medier osv. have i det.

Kapitel 4

Hvor får du nyheder fra? (1 lekt.)

Over tid er nyheder blevet tilgængelige langt flere steder end tidligere - og på alle tidspunkter af døgnet. Men der er også orskel på, hvor forskellige mennesker og grupper mest henter nyheder. Det skal I arbejde med i denne opgave.

Nedenfor finder I en statistik over, hvor danskere i forskellige aldersklasser får deres nyheder fra. I kan vælge at lave søjler eller kurver og se værdierne ved at markere dem.

Opgaver

  1. Tal i gruppen over, hvor I forventer, at flest får deres nyheder fra. Hvilken forskel forventer I at se mellem forskellige aldersgrupper?
  2. Klik de forskellige muligheder fra og til for at få et indtryk af, hvad statistikken viser. Svarer det til jeres forventninger?
  3. I hvilke typer har der været størst udvikling siden 2018? Hvad er steget mest, og hvad er faldet mest? Hvorfor tror I, det er gået sådan?
  4. Hvad gør de unge? Se på de 16-24-årige: Hvor får flest og færrest deres nyheder fra? 
  5. Kan I tænke på en fordel og en ulempe ved hver af de forkellige kilder til nyheder?

Stor eller lille udvikling?

De valg, man træffer, når man viser sine data i et diagram, er vigtige for, om modtageren får indtryk af en stor eller lille udvikling. I eksemplet nedenfor kan du trække i pilen og sammenligne to forskellige grafer, der viser, hvor mange der læser nyheder på sociale medier. De to grafer viser de samme tal. 

Opgaver

5. Hvad er forskellen på de to diagrammer?

6. Hvilke fordele kan der være ved at vise data på hver af de to måder? Hvorfor?

7. En graf kan give et misvisende indtryk. Hvilke interesser kunne politikere, sociale medier osv. have i det.

Kapitel 5

Unges uddannelser (1-2 lekt.)

Gæt selv

I de kommende år skal I træffe en række valg om jeres videre vej gennem uddannelsessystemet. 

Hvor mange tror I, der har gennemført en erhvervsuddannelse om året - og er antallet steget siden 2005? Erhvervsuddannelser er fx elektriker og politibetjent.

Gæt selv og tegn kurver for udviklingen for piger og drenge nedenunder. Du kan tjekke, hvor tæt du kom ved at trykke ”Se resultat”.

Grafen nedenunder viser, hvor mange der har afsluttet forskellige typer uddannelse hvert år siden 2005. I kan vælge at lave søjler eller kurver og se værdierne ved at markere dem. 

Uddannelsestyper

  • Grundskole:-10. klasse i folkeskole, fri- eller privatskole
  • Erhvervsuddannelser: Kan tages efter grundskolen. fx elektriker og frisør
  • Gymnasiale uddannelser: tager 2-3 år. Kan tages efter grundskolen. STX, HTX, HHX og HF
  • Korte videregående uddannelser: Varer typisk 1-2 år og bygger oven på en ungdomsuddannelse. Fx datamatiker eller tandplejer
  • Mellemlange videregående uddannelser: tager 2-4 år. Fx sygeplejerske og folkeskolelærer
  • Bacheloruddannelse: tager 3 år giver adgang til at fortsætte på en kandidatuddannelse. Fx en bachelor i engelsk eller en HA i erhvervsøkonomi.
  • Lange videregående uddannelser: eller kandidatuddannelse - varer mindst 2 år og fortsætter en bacheloruddannelse. Fx arkæolog og fysiker.
  • Ph.D.-uddannelse: En forskeruddannelse på 3 år, som kan tages efter en lang videregående uddannelse.

Opgaver

Klik de forskellige variable fra og til og undersøg:

  1. Hvilken type uddannelse gennemførte flest sidste år (se forklaring af typer ovenover)?
  2. Vælg 3 typer uddannelser og sammenlign udviklingen i, hvor mange der har taget dem siden 2005. Diskuter hvorfor udviklingen er sådan.
  3. Er der forskel på, hvilke uddannelser piger og drenge har gennemført?

Stor eller lille udvikling?

De valg, man træffer, når man viser sine data i et diagram, er vigtige for, om modtageren får indtryk af en stor eller lille udvikling. I eksemplet nedenfor kan du trække i pilen og sammenligne to forskellige grafer, der viser, hvor mange der er i gang med en gymnasial uddannelse. De to grafer viser de samme tal. 

Opgaver

4. Hvad er forskellen på de to diagrammer?

5. Hvilke fordele kan der være ved at vise data på hver af de to måder? Hvorfor?

6. En graf kan give et misvisende indtryk. Hvilke interesser kunne politikere, sociale medier osv. have i det.